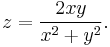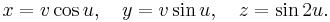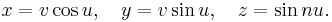Plücker's conoid

In geometry, the Plücker’s conoid is a ruled surface named after the German mathematician Julius Plücker. It is also called a cylindroid or conical wedge.

The Plücker’s conoid is defined by the function of two variables:

By using cylindrical coordinates in space, we can write the above functon into parametric equations

Thus the Plücker’s conoid is a right conoid, which can be obtained by rotating a horizontal line about the z-axis with the oscillatory motion (with period 2π) along the segment [−1, 1] of the axis (Figure 4).

A generalization of the Plücker’s conoid is given by the parametric equations

where n denotes the number of folds in the surface. The difference is that the period of the oscillatory motion along the z-axis is 2π/n. (Figure 5 for n = 3)

See also

• Ruled surface
• Right conoid

External links

• Plücker’s conoid from MathWorld

References

• A. Gray, E. Abbena, S. Salamon,Modern differential geometry of curves and surfaces with Mathematica, 3rd ed. Boca Raton, FL:CRC Press, 2006. [1] (ISBN 9781584884484)

• Vladimir Y. Rovenskii, Geometry of curves and surfaces with MAPLE [2] (ISBN 978-0-8176-4074-3)